Freemasonry |The Point Within a Circle

As
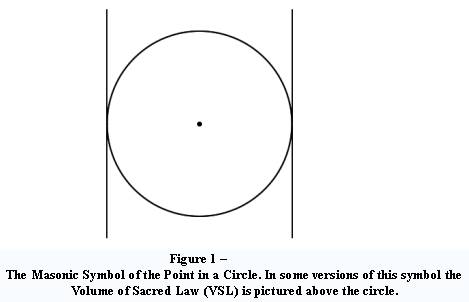
Masons, we are all introduced during our ritual lectures to the Masonic symbol
of the Point Within a Circle, and instructed in its’ allusion. 
The most interesting thing to me during my own such introduction was that
the figure representing this symbol contained not only a point within a circle,
but also two straight vertical lines touching the sides of the circle. It was
explained during the ensuing lecture that these lines represented the two Holy
Saints John, namely John the Baptist, and John the Evangelist. This struck me as
peculiar to say the least, and I have been trying to figure out this peculiarity
ever since.

 In
the course of my inquiry I found several explanations, including one[i]
which pointed out that the Feasts of the two Saint Johns are separated by six
months time, and that the symbol of the Point Within a Circle is a sort of
miniature ornery showing the path of the earth about the sun, with the feasts
designating winter and summer solstices[ii]. 
Another explanation likened the circle to an astronomical or astrological
diagram, complete with astrological symbols arranged about the circle
circumference, and which held that the vertical lines were representative of the
tropic of Cancer and the Tropic of Capricorn[iii].
Yet another variation[iv]
of the explanation of the Point Within a Circle also identified the vertical
lines as signifying the two Saints John, but expounded upon the significance of
the VSL in the symbol and offered an exhaustive discussion of chapters and
verses within the Bible attributed to Saint John the Baptist and St. John the
Evangelist all of which alluded to the Point Within a Circle representing God
and man, respectively. A further version was discovered which ignored the
vertical lines, but which asserted that the Pint Within a Circle was the Monad[v],
and represented God.

These
various explanations, though they were all plausible in the world of Masonic
symbolism, did not satisfy my curiosity. I began to consider that the figure
representing the point within a circle is reminiscent of a drawing which one
find in a textbook illustrating some principle of Geometry. We are all
acquainted with the Masonic symbol of the 47^th Proposition of Euclid;
I began to wonder if the point within a circle might be a similar construction.

It
was at about this time that through further reading I discovered what was
described as a closely held secret[vi]
of ancient craft Masons; namely that if one is to draw a circle and then draw a
further line across that circle through its’ center point (marking it’s
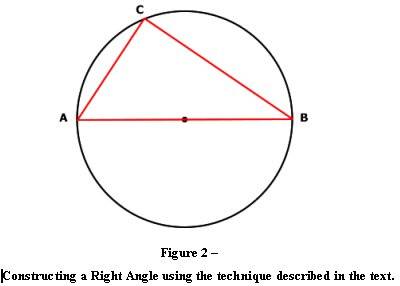
diameter) a right triangle can be simply yet consistently constructed. The
technique involved is to draw a line starting at the point where the line
through the circle center intersects the circle circumference (Point A in Figure
2), and to extend that line until it touches the circle at any point on its’
circumference (Figure 2, Point C). The line is then continued from the point of
intersection with the circumference to the point at which the center line
intersects the circle on the opposite side of the circles’ diameter (Figure 2,
Point B) and is further continued to the start (Figure 2, Point A). 
The end result is that a right triangle is constructed regardless of the
point on the circles’ circumference selected. Try it yourself, it works very
nicely.

This
method for the construction of a right angle is presented as Theorem
12, in Book III of Euclids’ Elements[vii] 
(Euclid, III. 3.), “An angle
inscribed in a semi-circle is a right angle”.  Euclid wrote: “Let angle ABC be inscribed in the semi-circle
ABC; that is, let AC be a diameter and let the vertex B lie on the circumference;
then angle ABC is a right angle”.  Although
presented in Euclids’ Elements and provided with a proof formulated by Euclid,
it was the Greek Philosopher, Astronomer, and Mathematician Thales of Miletus[viii]
(ca. 624 BC–ca. 546 BC), who is credited with the first publication of this
theorem.  

Naturally,
as a trade Secret this technique would have proven extremely valuable to the
ancient Craft Masons, and could be used among other things, to check the squares
of workmen to ensure that they were true. . It is also probable that the
development of scientific surveying and navigating instruments such as the
astrolabe made use of this, or a similar Theorem in their construction and as
their operating principle.

When
reading this I recalled the symbol of the Point Within a Circle, and began to
wonder if the Point Within a Circle might actually be a diagram which was
intended to be used as a proof of Thales’ Theorem. I decided to research the
matter and in the course of doing so, discovered an excerpt from a Masonic
Handbook[ix],
which (regarding the point within a circle) stated: 

“Ritualistically,
this is a symbol of control of conduct; a standard of right living. The symbol
has an extreme antiquity. Early Egyptian monuments are carved with the Alpha and
the Omega or symbol of God in the center of a circle embordered by two upright
parallel perpendicular serpents, representing the power and wisdom of the
Creator. The symbol apparently came into Masonry from an operative practice,
known to but a few Master workmen on Cathedrals and great buildings.

Any
school boy knows it now; put a dot on a circle anywhere; draw a straight line
across the circle through its center; connect the dot with the points at which
the line through the center cuts the circle; the result is a perfect square.

This
was the Operative Master’s great secret – knowing how to “try the square”
It was by this that he tested the working tools of the Fellows of the Craft; did
he do so often enough, it was impossible either for their tools or their work
“to materially err”.

I
nearly considered the matter settled, and was convinced that I had drawn the
correct conclusion thinking that the Point Within a Circle was a clue to the
Geometric construction by which Thales’ Theorem could be derived. 
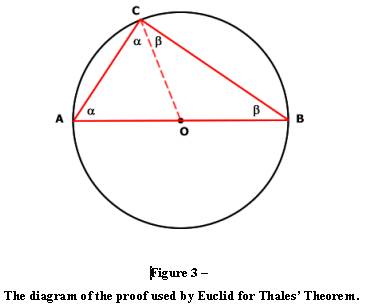
With further reflection I decided to confirm this by looking at the
published proof offered by Euclid.  I
was surprised to discover that the proof of the theorem did not involve the
construction of parallel tangent lines at all, but rather relied upon the
construction of a simple radius to the vertex producing the right angle[x]
(see Figure 3). Further investigation revealed that over the centuries there
have been numerous other proofs of the Theorem developed, all different from
that of Euclid, but none of them employing two parallel tangent lines.

           
I quickly began to suspect that Thales’ Theorem was not actually
related to the Point Within a Circle, but rather that the Point Within a Circle
was associated with a different Geometric construction. I combed Geometry
Textbooks, Masonic Encyclopedias, and the Internet searching for a Geometric
figure which was constructed using a circle, a point at the center of the circle,
and two parallel tangent lines on that circle. What I discovered was a second
method by which a right triangle could be constructed, using these very elements
along with one additional straight line, which is also a tangent to the circle.
I have reproduced this figure as described by my source[xi]
(Figure 4) below, along with an explanation of how the
figure is drawn.

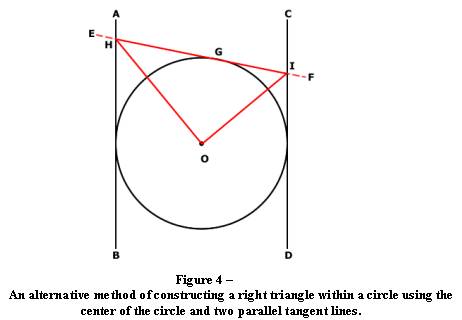
In
Figure 4, AB and CD are two parallel tangents to a circle having a center O. A
random tangent EF with point of contact G intersects AB at point H and CD at
point I. Beginning with the center of the circle O a line is drawn connecting O
with point H. The line is extended to connect point H to point I, and continued
back to the center of the circle, Point O. 
This construction produces a triangle in which angle HOI is 90^o. 

A
narrative description of this technique is that given a circle with two parallel
tangents, and a third tangent drawn randomly to the circle which intersects both
of the two parallel tangents, a right angle may be constructed by connecting the
center point of the circle to the points at which the tangents intersect. The
proof of this construction is similar to that used for Thales Theorem (see
footnote 9) and requires construction of a segment from the circle center O to
the tangent point G.

It
is, I believe quite amazing that the elements of this construction so neatly
utilize the framework contained within the Masonic symbol of a Point Within a
Circle.  This discovery however leads to other questions. For example,
why was this particular method for the construction of a right triangle used as
a Craft symbol, when a simpler method (Thales Theorem) existed, and was
chronicled by Euclid ?  If this
construction is indeed the intended functional use of the Point Within a Circle
symbol, it is probably of some importance to the Craft; yet this construction as
a Geometric function is fairly obscure and is not considered by Euclid as a
Theorem or Proposition (although several of Euclids’ propositions are used to
establish the proof). Answers to these questions remain to be discovered, and I
intend to find great entertainment in further exploration. A friend of mine once
said “Most of what I know I learned while looking up the answer to something
else”. The truth of that humorous comment is rarely more evident than when
examining the ancient symbols of our Craft.